August 27, 2024
P80 - Conversions.
(Warning! The introductory text below is quite long. If you are familiar with graphs, you might just look at source code in Graph.kt.)
A graph is defined as a set of nodes and a set of edges, where each edge is a pair of nodes.
The class to represent a graph is mutable, which isn't in keeping with pure functional programming, but a pure functional data structure would make things much, much more complicated. Pure functional graphs with cycles require laziness; Kotlin can probably handle it, but I think that would add too much of a barrier to the following questions.
Our graphs use an incidence list internally. Each has a list of nodes and a list of edges. Each node also has a list of edges that connect it to other nodes. In a directed graph, nodes, that are the target of arcs, do not have references to those arcs in their adjacency list.
class Graph<T, U> {
val nodes: MutableMap<T, Node<T, U>> = HashMap()
val edges: MutableList<Edge<T, U>> = ArrayList()
fun addNode(value: T): Node<T, U> {
val node = Node<T, U>(value)
nodes.put(value, node)
return node
}
fun addUndirectedEdge(n1: T, n2: T, label: U?) {
if (!nodes.contains(n1) || !nodes.contains(n2)) {
throw IllegalStateException("Expected '$n1' and '$n2' nodes to exist in graph")
}
val edge = UndirectedEdge(nodes[n1]!!, nodes[n2]!!, label)
if (edges.all{ !it.equivalentTo(edge) }) {
edges.add(edge)
nodes[n1]!!.edges.add(edge)
nodes[n2]!!.edges.add(edge)
}
}
fun addDirectedEdge(source: T, dest: T, label: U?) {
val edge = DirectedEdge(nodes[source]!!, nodes[dest]!!, label)
if (!edges.contains(edge)) {
edges.add(edge)
nodes[source]!!.edges.add(edge)
}
}
data class Node<T, U>(val value: T) {
val edges: MutableList<Edge<T, U>> = ArrayList()
fun neighbors(): List<Node<T, U>> = edges.map{ edge -> edge.target(this)!! }
override fun toString() = value.toString()
}
interface Edge<T, U> {
val n1: Node<T, U>
val n2: Node<T, U>
val label: U?
fun target(node: Node<T, U>): Node<T, U>?
fun equivalentTo(other: Edge<T, U>) =
(n1 == other.n1 && n2 == other.n2) || (n1 == other.n2 && n2 == other.n1)
}
data class UndirectedEdge<T, U>(override val n1: Node<T, U>, override val n2: Node<T, U>, override val label: U?) : Edge<T, U> {
override fun target(node: Node<T, U>) = if (n1 == node) n2 else if (n2 == node) n1 else null
override fun toString() = n1.toString() + "-" + n2 + (if (label == null) "" else "/" + label.toString())
}
data class DirectedEdge<T, U>(override val n1: Node<T, U>, override val n2: Node<T, U>, override val label: U?) : Edge<T, U> {
override fun target(node: Node<T, U>) = if (n1 == node) n2 else null
override fun toString() = n1.toString() + ">" + n2 + (if (label == null) "" else "/" + label.toString())
}
}
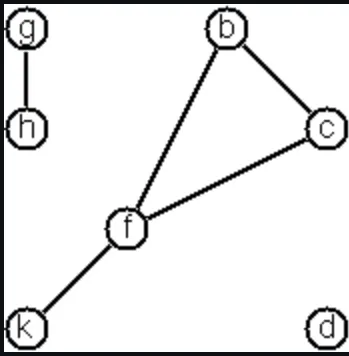
There are a few ways to create a graph from primitives. The graph-term form lists the nodes and edges separately:
Graph.terms(TermForm(
nodes = listOf("b", "c", "d", "f", "g", "h", "k"),
edges = listOf(Term("b", "c"), Term("b", "f"), Term("c", "f"), Term("f", "k"), Term("g", "h"))))The adjacency-list form associates each node with its adjacent nodes. In an undirected graph, care must be taken to ensure that all links are symmetric, i.e. if b is adjacent to c, c must also be adjacent to b.
Graph.adjacent(AdjacencyList(
Entry("b", links("c", "f")),
Entry("c", links("b", "f")),
Entry("d"),
Entry("f", links("b", "c", "k")),
Entry("g", links("h")),
Entry("h", links("g")),
Entry("k", links("f"))))The representations we introduced so far are bound to our implementation and therefore well suited for automated processing, but their syntax is not very user-friendly. Typing the terms by hand is cumbersome and error-prone. We can define a more compact and "human-friendly" notation as follows: A graph is represented by a string of terms of the type X or Y-Z separated by commas. The standalone terms stand for isolated nodes, the Y-Z terms describe edges. If an X appears as an endpoint of an edge, it is automatically defined as a node. Our example could be written as:
[b-c, f-c, g-h, f-b, k-f, h-g, d]
We call this the human-friendly form. As the example shows, the list does not have to be sorted and may even contain the same edge multiple times. Notice the isolated node d.
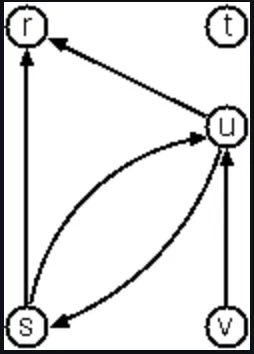
Directed graph is a graph where edges have direction. To represent a directed graph, the forms discussed above are slightly modified. The example graph is represented as follows:
In graph-term form:
Graph.directedTerms(TermForm(
listOf("r", "s", "t", "u", "v"),
listOf(Term("s", "r"), Term("s", "u"), Term("u", "r"), Term("u", "s"), Term("v", "u"))))In adjacency-list form (note that the adjacency-list form is the same for graphs and digraphs):
Graph.directedAdjacent(AdjacencyList(
Entry("r"),
Entry("s", links("r", "u")),
Entry("t"),
Entry("u", links("r", "s")),
Entry("v", links("u"))))Human-friendly form:
[s>r, s>u, u>r, u>s, v>u, t]
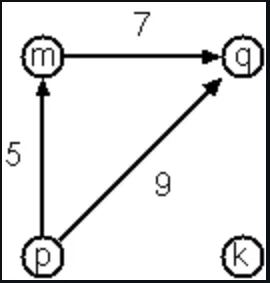
Finally, graphs with additional information attached to edges are called labeled graphs.
Graph-term form:
Graph.labeledTerms(TermForm(
listOf("k", "m", "p", "q"),
listOf(Term("m", "q", 7), Term("p", "m", 5), Term("p", "q", 9))))Adjacency-list form:
Graph.labeledDirectedAdjacent(AdjacencyList(
Entry("k"),
Entry("m", Link("q", 7)),
Entry("p", Link("m", 5), Link("q", 9)),
Entry("q")))Human-friendly form:
[m-q/7, p-m/5, p-q/9, k]
The notation for labeled graphs can also be used for so-called multi-graphs, where more than one edge is allowed between two given nodes.
Write String.toGraph() and String.toLabeledGraph() functions to create graphs from strings (you can detect if graph is labeled or unlabeled based on input string format). Write functions toTermForm and toAdjacencyList to generate the graph-term and adjacency-list forms of a Graph.
> "[b-c, b-f, c-f, f-k, g-h, d]".toGraph().toTermForm()
TermForm(nodes=[f, g, d, b, c, k, h], edges=[Term(b, c), Term(b, f), Term(c, f), Term(f, k), Term(g, h)])
> "[m>q/7, p>m/5, p>q/9, k]".toLabeledGraph().toAdjacencyList()
AdjacencyList(Entry("q"), Entry("p", listOf(Link("q", 9), Link("m", 5))), Entry("m", listOf(Link("q", 7))), Entry("k"))kotlin
package org.kotlin99.graphs
import com.natpryce.hamkrest.MatchResult
import com.natpryce.hamkrest.MatchResult.Match
import com.natpryce.hamkrest.MatchResult.Mismatch
import com.natpryce.hamkrest.Matcher
import com.natpryce.hamkrest.assertion.assertThat
import com.natpryce.hamkrest.describe
import com.natpryce.hamkrest.equalTo
import org.junit.Test
import org.kotlin99.common.containsAll
import org.kotlin99.graphs.Graph.AdjacencyList
import org.kotlin99.graphs.Graph.AdjacencyList.Entry
import org.kotlin99.graphs.Graph.AdjacencyList.Entry.Companion.links
import org.kotlin99.graphs.Graph.AdjacencyList.Link
import org.kotlin99.graphs.Graph.TermForm
import org.kotlin99.graphs.Graph.TermForm.Term
import org.kotlin99.graphs.GraphTest.Companion.assertPropertiesOfDirectedGraphExample
import org.kotlin99.graphs.GraphTest.Companion.assertPropertiesOfDirectedLabeledGraphExample
import org.kotlin99.graphs.GraphTest.Companion.assertPropertiesOfUndirectedGraphExample
import org.kotlin99.graphs.GraphTest.Companion.assertPropertiesOfUndirectedLabeledGraphExample
import java.util.*
import java.util.regex.Pattern
private val graphTokenSeparators = Pattern.compile("[->/]")
fun String.toGraph(): Graph<String, Nothing> {
if (!startsWith('[') || !endsWith(']')) {
throw IllegalArgumentException("Expected string starting '[' and ending with ']' but it was '$this'")
}
val tokens = substring(1, length - 1).split(", ").map { it.split(graphTokenSeparators) }
val nodes = tokens.flatten().toCollection(LinkedHashSet())
val edges = tokens.filter { it.size == 2 }.map { Term<String, Nothing>(it[0], it[1]) }
return if (contains("-")) {
Graph.terms(TermForm(nodes, edges))
} else {
Graph.directedTerms(TermForm(nodes, edges))
}
}
fun String.toLabeledGraph(): Graph<String, Int> {
if (!startsWith('[') || !endsWith(']')) {
throw IllegalArgumentException("Expected string starting '[' and ending with ']' but it was '$")
}
val tokens = substring(1, length - 1).split(", ").map { it.split(graphTokenSeparators) }
val nodes = tokens.flatMap { it.take(2) }.toCollection(LinkedHashSet())
val edges = tokens.filter { it.size == 3 }.map { Term(it[0], it[1], it[2].toInt()) }
return if (contains("-")) {
Graph.labeledTerms(TermForm(nodes, edges))
} else {
Graph.labeledDirectedTerms(TermForm(nodes, edges))
}
}
fun <V, L> Graph<V, L>.toTermForm(): TermForm<V, L> {
val nodeValues = nodes.values.map { it.value }
val terms = edges.map { Term(it.n1.value, it.n2.value, it.label) }
return TermForm(nodeValues, terms)
}
fun <V, L> Graph<V, L>.toAdjacencyList(): AdjacencyList<V, L> {
val entries = nodes.values.map { node ->
val links = node.edges.map { Link(it.target(node)!!.value, it.label) }
Entry(node = node.value, links = links)
}
return AdjacencyList(entries)
}
class P80Test {
@Test fun `graph conversion from and to string`() {
"[b-c, b-f, c-f, f-k, g-h, d]".toGraph().assertPropertiesOfUndirectedGraphExample()
"[s>r, s>u, u>r, u>s, v>u, t]".toGraph().assertPropertiesOfDirectedGraphExample()
"[m-q/7, p-m/5, p-q/9, k]".toLabeledGraph().assertPropertiesOfUndirectedLabeledGraphExample()
"[m>q/7, p>m/5, p>q/9, k]".toLabeledGraph().assertPropertiesOfDirectedLabeledGraphExample()
}
@Test fun `graph equality and equivalence`() {
assertThat("[a]".toGraph(), equalTo("[a]".toGraph()))
assertThat("[a]".toGraph(), !equalTo("[b]".toGraph()))
assertThat("[a-b]".toGraph(), equalTo("[a-b]".toGraph()))
assertThat("[a-b]".toGraph(), !equalTo("[b-a]".toGraph()))
assertThat("[a-b]".toGraph(), equivalentTo("[a-b]".toGraph()))
assertThat("[a-b]".toGraph(), equivalentTo("[b-a]".toGraph()))
assertThat("[a-b, b-c]".toGraph(), equivalentTo("[c-b, b-a]".toGraph()))
}
@Test fun `convert graph to term form`() {
assertThat("[b-c, b-f, c-f, f-k, g-h, d]".toGraph().toTermForm(), equalTo(TermForm(
listOf("b", "c", "f", "k", "g", "h", "d"),
listOf(Term("b", "c"), Term("b", "f"), Term("c", "f"), Term("f", "k"), Term("g", "h"))
)))
}
@Test fun `convert graph to adjacency list`() {
assertThat("[a-b, a-c]".toGraph().toAdjacencyList(), equalTo(AdjacencyList(
Entry("a", links("b", "c")),
Entry("b", links("a")),
Entry("c", links("a"))
)))
assertThat("[b-c, b-f, c-f, f-k, g-h, d]".toGraph().toAdjacencyList(), equalTo(AdjacencyList(
Entry("b", links("c", "f")),
Entry("c", links("b", "f")),
Entry("d"),
Entry("f", links("b", "c", "k")),
Entry("g", links("h")),
Entry("h", links("g")),
Entry("k", links("f"))
)))
assertThat("[m-q/7, p-m/5, p-q/9, k]".toLabeledGraph().toAdjacencyList(), equalTo(AdjacencyList(
Entry("q", listOf(Link("m", 7), Link("p", 9))),
Entry("p", listOf(Link("m", 5), Link("q", 9))),
Entry("m", listOf(Link("q", 7), Link("p", 5))),
Entry("k")
)))
}
private fun <V, L> equalTo(expected: AdjacencyList<V, L>): Matcher<AdjacencyList<V, L>> {
return object: Matcher.Primitive<AdjacencyList<V, L>>() {
override fun invoke(actual: AdjacencyList<V, L>) = containsAll(expected.entries).invoke(actual.entries)
override val description: String get() = "has the same elements as ${describe(expected)}"
override val negatedDescription: String get() = "element are not the same as in ${describe(expected)}"
}
}
companion object {
fun <V, L> equivalentTo(expected: Graph<V, L>): Matcher<Graph<V, L>> =
object: Matcher<Graph<V, L>> {
override fun invoke(actual: Graph<V, L>): MatchResult =
if (actual.equivalentTo(expected)) Match else Mismatch("was ${describe(actual)}")
override val description: String get() = "is equivalent to ${describe(expected)}"
override val negatedDescription: String get() = "is not equivalent to ${describe(expected)}"
}
}
}