August 27, 2024
P84 - Minimum spanning tree.
Write a method minSpanningTree to construct the minimum spanning tree of a given labeled graph. Hint: Use Prim's Algorithm.
> "[a-b/1, b-c/2, a-c/3]".toLabeledGraph().minSpanningTree()
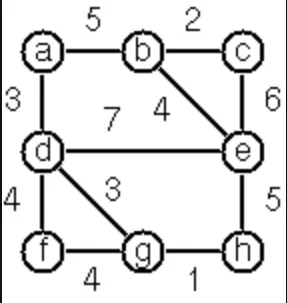
[a-b/1, b-c/2]Find minimum spanning tree for the graph below:
"[a-b/5, a-d/3, b-c/2, b-e/4, c-e/6, d-e/7, d-f/4, d-g/3, e-h/5, f-g/4, g-h/1]".toLabeledGraph()kotlin
package org.kotlin99.graphs
import com.natpryce.hamkrest.assertion.assertThat
import com.natpryce.hamkrest.equalTo
import org.junit.Test
import org.kotlin99.common.tail
import org.kotlin99.graphs.Graph.Edge
import org.kotlin99.graphs.Graph.Node
import org.kotlin99.graphs.P80Test.Companion.equivalentTo
import java.util.*
fun <V, L: Comparable<L>> Graph<V, L>.minSpanningTree(): Graph<V, L> {
fun Edge<V, L>.contains(node: Node<V, L>) = n1 == node || n2 == node
fun Edge<V, L>.connectsTo(nodes: List<Node<V, L>>) = nodes.contains(n1) != nodes.contains(n2)
// Comparator is only required for tree without labels (i.e. with null label values).
val comparator = Comparator<Edge<V, L>> { e1, e2 ->
if (e1.label == null && e2.label == null) 0
else if (e1.label == null) -1
else if (e2.label == null) 1
else e1.label?.compareTo(e2.label!!)!!
}
fun minSpanningTree(graphEdges: List<Edge<V, L>>, graphNodes: List<Node<V, L>>): Graph<V, L> {
return if (graphNodes.isEmpty()) {
Graph(nodes.values, edges - graphEdges)
} else {
val edge = graphEdges.filter { it.connectsTo(graphNodes) }.minWithOrNull(comparator)!!
minSpanningTree(
graphEdges.filterNot { it == edge },
graphNodes.filterNot { edge.contains(it) }
)
}
}
return minSpanningTree(edges, nodes.values.tail())
}
class P84Test {
@Test fun `minimum spanning tree`() {
assertThat("[a-b/1]".toLabeledGraph().minSpanningTree(), equivalentTo("[a-b/1]".toLabeledGraph()))
assertThat("[a-b/1, b-c/2]".toLabeledGraph().minSpanningTree(), equivalentTo("[a-b/1, b-c/2]".toLabeledGraph()))
assertThat("[a-b/1, b-c/2, a-c/3]".toLabeledGraph().minSpanningTree(), equivalentTo("[a-b/1, b-c/2]".toLabeledGraph()))
}
@Test fun `minimum spanning tree for unlabeled graph`() {
assertThat("[a-b]".toGraph().minSpanningTree(), equivalentTo("[a-b]".toGraph()))
assertThat("[a-b, b-c]".toGraph().minSpanningTree(), equivalentTo("[a-b, b-c]".toGraph()))
assertThat("[a-b, b-c, a-c]".toGraph().minSpanningTree(), equivalentTo("[a-b, b-c]".toGraph()))
}
@Test fun `minimum spanning tree for graph from illustration`() {
val graph = "[a-b/5, a-d/3, b-c/2, b-e/4, c-e/6, d-e/7, d-f/4, d-g/3, e-h/5, f-g/4, g-h/1]".toLabeledGraph()
assertThat(graph.minSpanningTree(), equivalentTo("[d-f/4, a-d/3, d-g/3, g-h/1, a-b/5, b-c/2, b-e/4]".toLabeledGraph()))
assertThat(graph.minSpanningTree().edges.sumOf { it.label!! }, equalTo(22))
}
}