August 27, 2024
P92 - Von Koch's conjecture (see also graceful labeling).
Several years ago I met a mathematician who was intrigued by a problem for which he didn't know a solution. His name was Von Koch, and I don't know whether the problem has been solved since. (The "I" here refers to the author of the Prolog problems.)
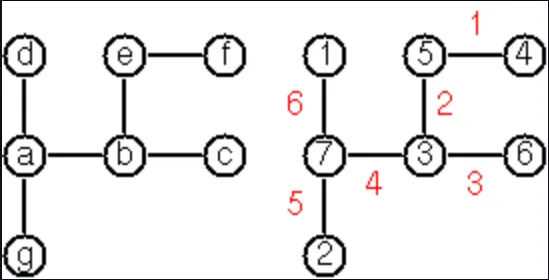
Anyway the puzzle goes like this: Given a tree with N nodes (and hence N-1 edges), find a way to enumerate the nodes from 1 to N and, accordingly, the edges from 1 to N-1 in such a way, that for each edge K the difference of its node numbers is equal to K. The conjecture is that this is always possible.
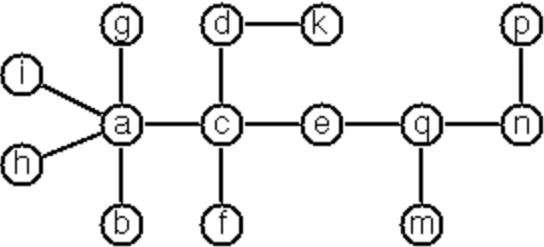
For small trees the problem is easy to solve by hand. However, it is extremely difficult to find a solution for larger trees, and 14 is already very large. And remember, we don't know for sure whether there is always a solution!
Write a function that calculates a numbering scheme for a given tree. What is the solution for the larger tree pictured below?
kotlin
package org.kotlin99.misc
import com.natpryce.hamkrest.anyElement
import com.natpryce.hamkrest.assertion.assertThat
import com.natpryce.hamkrest.equalTo
import org.junit.Test
import org.kotlin99.common.containsAll
import org.kotlin99.common.permutationsSeq
import org.kotlin99.graphs.Graph
import org.kotlin99.graphs.Graph.TermForm
import org.kotlin99.graphs.Graph.TermForm.Term
import org.kotlin99.graphs.toGraph
import org.kotlin99.graphs.toTermForm
import java.util.*
import kotlin.math.abs
fun <V> Graph<V, *>.gracefulLabeling(): Sequence<Graph<String, Nothing>> {
val edgeLabels = 1.rangeTo(edges.size).toHashSet()
return 1.rangeTo(nodes.size).toList()
.permutationsSeq()
.map { nodeLabels -> nodes.keys.zip(nodeLabels).toMap() }
.filter { mapping ->
val diffs = edges.mapTo(HashSet()) { edge ->
abs(mapping.getValue(edge.n1.value) - mapping.getValue(edge.n2.value))
}
diffs == edgeLabels
}
.map { mapping ->
toTermForm().run {
Graph.terms(TermForm(
nodes.map { mapping.getValue(it).toString() },
edges.map { Term(mapping.getValue(it.n1).toString(), mapping.getValue(it.n2).toString()) }
))
}
}
}
class P92Test {
@Test fun `basic graceful labeling`() {
assertThat("[a]".toGraph().gracefulLabeling().first(), equalTo("[1]".toGraph()))
assertThat("[a-b]".toGraph().gracefulLabeling().toList(), containsAll("[1-2]".toGraph(), "[2-1]".toGraph()))
assertThat("[a-b, a-c]".toGraph().gracefulLabeling().toList(), containsAll(
"[1-2, 1-3]".toGraph(), "[1-3, 1-2]".toGraph(),
"[3-1, 3-2]".toGraph(), "[3-2, 3-1]".toGraph()
))
}
@Test fun `graceful labeling of examples in readme`() {
assertThat("[a-d, a-g, a-b, b-c, b-e, e-f]".toGraph().gracefulLabeling().toList(), anyElement(equalTo(
"[7-2, 7-1, 7-3, 3-6, 3-5, 5-4]".toGraph()
)))
// TODO too slow
// assertThat("[a-i, a-h, a-g, a-b, a-c, c-f, c-d, d-k, c-e, e-g, g-m, g-n, n-p]".toGraph().gracefulLabeling().first(), equalTo(
// "[7-2, 7-1, 7-3, 3-6, 3-5, 5-4]".toGraph()
// ))
}
}