August 19, 2024
P64 - Layout a binary tree (1)
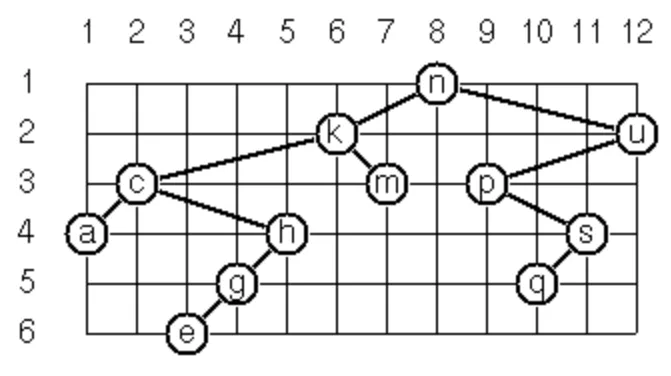
Consider a binary tree as the usual symbolic expression (X L R) or nil. As a preparation for drawing the tree, a layout algorithm is required to determine the position of each node in a rectangular grid. Several layout methods are conceivable, one of them is shown in the illustration below.
In this layout strategy, the position of a node v is obtained by the following two rules:
- x(v) is equal to the position of the node v in the inorder sequence
- y(v) is equal to the depth of the node v in the tree
In order to store the position of the nodes, we extend the symbolic expression representing a node (and its successors) as follows:nil represents the empty tree (as usual)
(W X Y L R) represents a (non-empty) binary tree with root W "positioned" at (X,Y), and subtrees L and R
Write a function layout-binary-tree with the following specification:
(layout-binary-tree tree) returns the "positioned" binary tree obtained from the binary tree tree
Test your function in an appropriate way.
lisp
(defun layout-binary-tree (tree)
(if (null tree)
nil
(let ((lsize (size (second tree))))
(list
(first tree)
(1+ lsize)
1
(add-to-y-coord
1
(layout-binary-tree (second tree))
)
(add-to-y-coord
1
(add-to-x-coord (1+ lsize) (layout-binary-tree (third tree)))
)
)
)
)
)
(defun size (tree)
(if (null tree)
0
(+ 1 (size (second tree)) (size (third tree)))
)
)
(defun add-to-x-coord (k tree)
(if (null tree)
nil
(list
(first tree)
(+ k (second tree))
(third tree)
(add-to-x-coord k (fourth tree))
(add-to-x-coord k (fifth tree))
)
)
)
(defun add-to-y-coord (k tree)
(if (null tree)
nil
(list
(first tree)
(second tree)
(+ k (third tree))
(add-to-y-coord k (fourth tree))
(add-to-y-coord k (fifth tree))
)
)
)
(setf tt '(n (k (c (a nil nil) (h (g (e nil nil) nil) nil)) (m nil nil)) (u (p nil (s (q nil nil) nil)) nil)))