August 21, 2024
P80 - Conversions
There are several ways to represent graphs in Lisp.
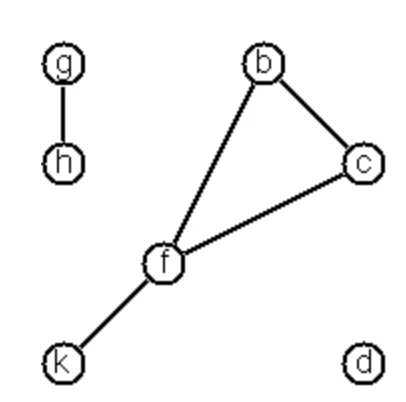
One method is to represent the whole graph as one data object. According to the definition of the graph as a pair of two sets (nodes and edges), we may use the following Lisp expression to represent the example graph:
((b c d f g h k) ( (b c) (b f) (c f) (f k) (g h) ))
We call thisgraph-expression form. Note, that the lists are kept sorted, they are really sets, without duplicated elements. Each edge appears only once in the edge list; i.e. an edge from a node x to another node y is represented as (x y), the expression (y x) is not present. The graph-expression form is our default representation.In Common Lisp there are predefined functions to work with sets.
A third representation method is to associate with each node the set of nodes that are adjacent to that node. We call this the adjacency-list form. In our example:
( (b (c f)) (c (b f)) (d ()) (f (b c k)) ...)
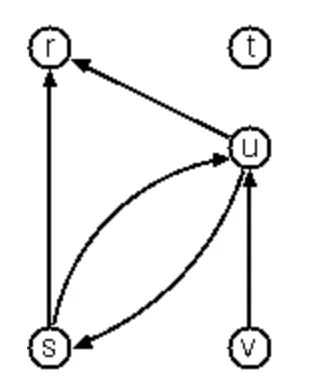
When the edges are directed we call them arcs. These are represented by ordered pairs. Such a graph is called directed graph. To represent a directed graph, the forms discussed above are slightly modified. The example graph opposite is represented as follows:
Graph-expression form( (r s t u v) ( (s r) (s u) (u r) (u s) (v u) ) )Adjacency-list form( (r ()) (s (r u)) (t ()) (u (r)) (v (u)) )Note that the adjacency-list does not have the information on whether it is a graph or a digraph.
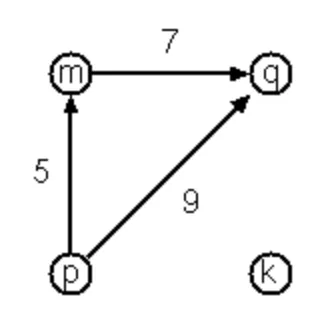
Finally, graphs and digraphs may have additional information attached to nodes and edges (arcs). For the nodes, this is no problem, as we can easily replace the single symbol identifiers with arbitrary symbolic expressions, such as ("London" 4711). On the other hand, for edges we have to extend our notation. Graphs with additional information attached to edges are called labelled graphs.
Graph-expression form( (k m p q) ( (m p 7) (p m 5) (p q 9) ) )
Adjacency-list form( (k ()) (m ((q 7))) (p ((m 5) (q 9))) (q ()) )
Notice how the edge information has been packed into a list with two elements, the corresponding node and the extra information.
The notation for labelled graphs can also be used for so-called multi-graphs, where more than one edge (or arc) are allowed between two given nodes.
Write functions to convert between the different graph representations. With these functions, all representations are equivalent; i.e. for the following problems you can always pick freely the most convenient form. The reason this problem is rated (***) is not because it's particularly difficult, but because it's a lot of work to deal with all the special cases.
lisp
(defun ge-to-al (graph)
(mapcar #'(lambda (x) (list x (adj-list graph x))) (car graph))
)
(defun adj-list (graph node)
(apply #'append (mapcar #'(lambda (x) (neighbor x node)) (second graph)))
)
(defun neighbor (pair node)
(cond
((eql node (first pair)) (list (second pair)))
((eql node (second pair)) (list (first pair)))
(t ())
)
)