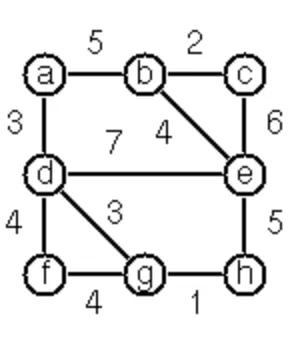
P84 - Construct a minimum spanning tree
Write a function (ms-tree graph) to construct a minimum spanning tree of a given labelled graph. The function must also return the minimum weight.
Hint: Use the algorithm of Prim. A small modification of the solution of P83 does the trick. The data of the example graph to the right can be found in the file p84.dat.
lisp
;;; MST by Prim
;;; Uses hashtable for the heap of 'bids'
;;; Takes graphs in adjacency list form
(defun ms-tree (graph)
(mst-aux graph
nil
(update graph
(first (first graph))
(make-hash-table)
()
)
)
)
(defun mst-aux (graph tree bids)
(if (= (hash-table-count bids) 0)
tree
(let* ((new (best graph bids))
(prior (first (gethash new bids))))
(mst-aux graph
(cons (list new prior) tree)
(update graph new bids (cons new (cons prior (nodes tree))))
)
)
)
)
(defun update (graph node bids processed)
(remhash node bids)
(dolist (pair (neighbors node graph) bids)
(let ((n (first pair))
(weight (weight pair)))
(if (and
(not (member n processed))
(or (not (gethash n bids))
(< weight (second (gethash n bids))))
)
(setf (gethash n bids) (list node weight))
)
)
)
)
(defun neighbors (node graph)
(second (first (member-if #'(lambda (x) (eql node (car x))) graph)))
)
(defun best (graph bids)
(minweight (mapcar #'car graph) bids)
)
(defun minweight (nodes bids)
(minweight-aux (cdr nodes) bids (car nodes))
)
(defun minweight-aux (nodes bids a)
(if (null nodes)
a
(minweight-aux (cdr nodes)
bids
(if (better (weight (gethash a bids))
(weight (gethash (car nodes) bids))
)
a
(car nodes)
)
)
)
)
(defun weight (x)
(second x)
)
(defun better (x y)
"Compares X to Y, which can be real numbers or NIL. BETTER means
smaller, or, if any is NIL, then the other is better. If both are nil
it does not matter: return anything"
(if (null x)
nil
(if (null y)
t
(<= x y)
)
)
)
(defun nodes (tree)
(apply #'append tree)
)