August 21, 2024
P92 - Von Koch's conjecture
Several years ago I met a mathematician who was intrigued by a problem for which he didn't know a solution. His name was Von Koch, and I don't know whether the problem has been solved since.
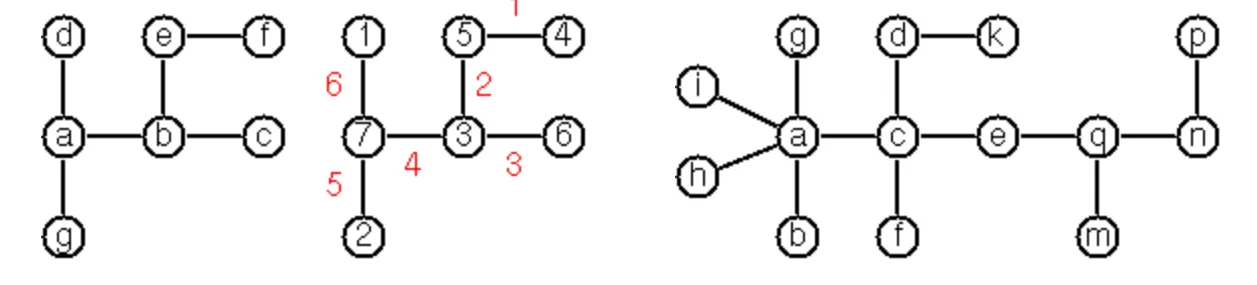
Anyway the puzzle goes like this: given a tree with N nodes (and hence N-1 edges), find a way to enumerate the nodes from 1 to N and, accordingly, the edges from 1 to N-1 in such a way that, for each edge K, the difference of its node numbers equals K. The conjecture is that this is always possible.
For small trees the problem is easy to solve by hand. However, for larger trees, and 14 is already very large, it is extremely difficult to find a solution. And remember, we don't know for sure whether there is always a solution!
Write a function that calculates a numbering scheme for a given tree. What is the solution for the larger tree pictured above?
lisp
;;; Graceful Labeling (Von Koch's conjecture)
;;; like a dfs, but assinging and verifying labels
;;; takes a tree in graph-expression form
(load "p80.lisp")
(load "p87.lisp")
(defun graceful-labeling (tree)
"Returns a graceful label for TREE if one exists. Node labels
go from 1 to length of TREE; edge labels go from 1 to one less
than length of TREE."
(let* ((list (ordered-edges tree))
(n (nnodes tree))
(seq (seq 1 n))
;; who has label is always the second of the pair
(tenta-node (cadar list) list nil seq (seq 1 (1-n)) seq)
)
)
(defun try-node (node list trib node-labels edge-labels a-try)
"Returns an assignment that completes the ATTRIB, with new labels
taken from NODE-LABELS for us, and EDGE-LABELS for edges, for
since the NODE label has to be one of the labels in A-TENTAR
if it exists; if it does not exist, it returns NIL.
LIST is the list of edges that need to be labeled."
(if (null a-try)
nil
(or (extends list
(acons node (car a-tempt) trib)
(remove (car a-try) node-labels)
edge-labels
)
(tenta-node node list trib node-labels edge-labels (cdr a-try))
)
)
)
(defun extends (dort list node-labels edge-labels)
"Returns an assignment that completes the ATTRIB, with new labels
taken from NODE-LABELS for us, and EDGE-LABELS for edges, for
if there is; otherwise, returns NIL.
LIST is the list of edges that need to be labeled."
(if (null list)
trib
(try (car list)
(cdr list)
trib
node-labels
edge-labels
node-labels)
)
)
(defun tries (pair list trib node-labels edge-labels a-try)
"Returns an assignment that completes the ATTRIB, with new labels
taken from NODE-LABELS for us, and EDGE-LABELS for edges, for
being that PAIR is the next edge trying, and it is known that the
second element of PAIR jah has label, while that label
of the first element of PAIR has to be one of the labels in A-TRY.
if there is no such atrbution, returns NIL.
LIST is the list of edges that need to be labeled, in addition to PAIR."
(if (null a-try)
nil
(let* ((a (second pair)) ; jah has label
(b (first pair)); has no label
(d (abs (- (car a-tempt) (cdr (assoc a trib))))
)
(or (and (member d edge-labels)
(extends list
(acons b (car a-tempt) trib)
(remove (car a-try) node-labels)
(remove edge-labels)
)
)
(try pair list trib node-labels edge-labels (cdr a-try))
)
)
)
)
(defun ordered-edges (tree)
"Returns the list of tree TREE edges ordered in such a way that,
from the second edge of the list, each edge has exactly one
element that has appeared before, and exactly one that has not appeared before.
DFS can be used to obtain such a list."
(let ((dfs (dfs (ge-to-al tree) (caar tree)))
(cdr
(mapcar #'(lambda (x) (list x (my-first-neighbor x tree dfs))
dfs)
)
)
(defun my-first-neighbor (node tree order)
"Returns first TREE-neighbor of NODE in ORDER, or nil if none exists."
(if (null order)
nil
(if (adjacent (car order) node tree)
(car order)
(my-first-neighbor node tree (cdr order))
)
)
)
(defun adjacent (a b tree)
(or (member (list a b) (second tree) :test #'equal)
(member (list b a) (second tree) :test #'equal)
)
)
(defun nnodes (tree)
(length (car tree))
)
(defun seq (a b)
(if (< b a)
nil
(cons a (seq (1+ a) b))
)
)