August 21, 2024
P99 - Crossword puzzle
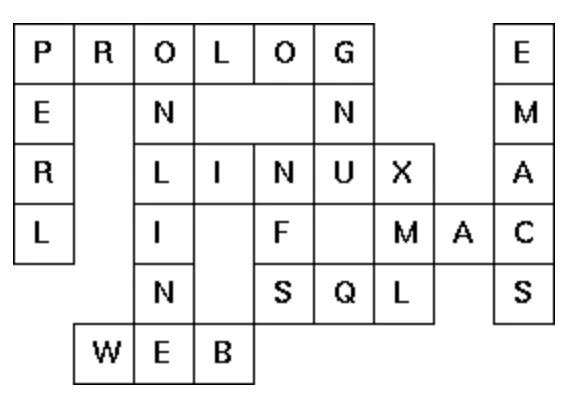
Given an empty (or almost empty) framework of a crossword puzzle and a set of words. The problem is to place the words into the framework.
The particular crossword puzzle is specified in a text file which first lists the words (one word per line) in an arbitrary order. Then, after an empty line, the crossword framework is defined. In this framework specification, an empty character location is represented by a dot (.). In order to make the solution easier, character locations can also contain predefined character values. The puzzle opposite is defined in the file p99a.dat, other examples are p99b.dat and p99d.dat. There is also an example of a puzzle (p99c.dat) which does not have a solution.
Words are strings (character lists) of at least two characters. A horizontal or vertical sequence of character places in the crossword puzzle framework is called a site. Our problem is to find a compatible way of placing words onto sites.
Hints:
(1) The problem is not easy. You will need some time to thoroughly understand it. So, don't give up too early! And remember that the objective is a clean solution, not just a quick-and-dirty hack!
(2) Reading the data file is a tricky problem for which a solution is provided in the file p99-readfile.lisp. Use the function read-lines, which returns the words and the grid in a 2-element list.
(3) For efficiency reasons it is important, at least for larger puzzles, to sort the words and the sites in a particular order. For this part of the problem, the solution of P28 may be very helpful.
lisp
;;; the idea here is to represent the problem as a graph G = (V,E), and
;;; where V is the set of sites and E are the sites that touch each other.
;;
;;; the graph would be oriented, always containing pairs of opposite edges
;;; and represented as adjacency lists.
;;
;;; Associados to each vertice (site) we have: its length and the
;;; positions already with defined characters; the other positions
;;; they would be free.
;;
;;; associated with each edge we would have: the position on site 1 and the position
;;; on site 2; positions start, from zero.
;;
;;; Basically, the solution uses a width search in the graph, with
;;; backtrack. With each visit in a vertice, all the words of the
;;; right size and matching to the already defined characters are
;;; attempted, in the order of the word list of the entry.
;;
;;; There is also a complementary part of the reading, where the
;;; graph and a hash of words by size.