P92 - Von Koch’s conjecture.

Several years ago I met a mathematician who was intrigued by a problem for which he didn’t know a solution.  His name was Von Koch, and I don’t know whether the problem has been solved since.  [The “I” here refers to the author of the Prolog problems.  <PMG>]

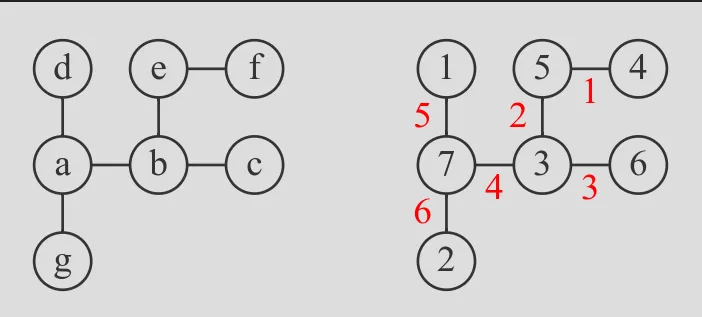
Anyway the puzzle goes like this: Given a tree with NN nodes (and hence N−1N−1 edges), find a way to enumerate the nodes from 1 to NN and, accordingly, the edges from 1 to N−1N−1 in such a way, that for each edge KK the difference of its node numbers is equal to KK.  The conjecture is that this is always possible.

For small trees the problem is easy to solve by hand.  However, for larger trees, and 14 is already very large, it is extremely difficult to find a solution.  And remember, we don’t know for sure whether there is always a solution!

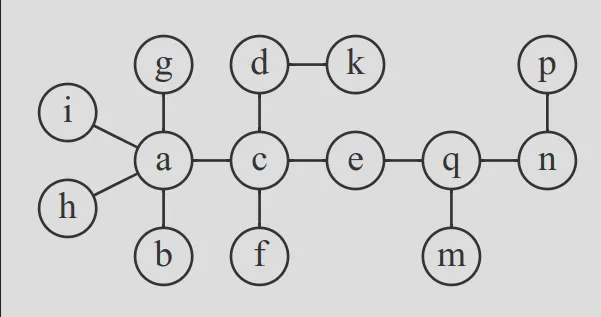
Write a function that calculates a numbering scheme for a given tree.  What is the solution for the larger tree pictured below?